(1)设计一个算法,确定两个矩形是否相交(即有重叠区域)
(2)如果两个矩形相交,设计一个算法,求出相交的区域矩形
(1) 对于这个问题,一般的思路就是判断一个矩形的四个顶点是否在另一个矩形的区域内。这个思路最简单,但是效率不高,并且存在错误,错误在哪里,下面分析一 下。
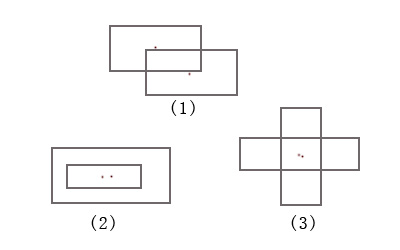
如上图,把矩形的相交(区域重叠)分成三种(可能也有其他划分),对于第三种情况,如图中的(3),两个矩形相交,但并不存在一个矩形的顶点在另一个矩形 内部。所以那种思路存在一个错误,对于这种情况的相交则检查不出。
仔细观察上图,想到另一种思路,那就是判断两个矩形的中心坐标的水平和垂直距离,只要这两个值满足某种条件就可以相交。
矩形A的宽 Wa = Xa2-Xa1 高 Ha = Ya2-Ya1
矩形B的宽 Wb = Xb2-Xb1 高 Hb = Yb2-Yb1
矩形A的中心坐标 (Xa3,Ya3) = ( (Xa2+Xa1)/2 ,(Ya2+Ya1)/2 )
矩形B的中心坐标 (Xb3,Yb3) = ( (Xb2+Xb1)/2 ,(Yb2+Yb1)/2 )
所以只要同时满足下面两个式子,就可以说明两个矩形相交。1) | Xb3-Xa3 | <= Wa/2 + Wb/2
2) | Yb3-Ya3 | <= Ha/2 + Hb/2
即:
| Xb2+Xb1-Xa2-Xa1 | <= Xa2-Xa1 + Xb2-Xb1
| Yb2+Yb1-Ya2-Ya1 | <=Y a2-Ya1 + Yb2-Yb1
(2) 对于这个问题,假设两个矩形相交,设相交之后的矩形为C,且矩形C的左上角坐标为(Xc1,Yc1),右下角坐标为(Xc2,Yc2),经过观察上图,很 显然可以得到:
Xc1 = max(Xa1,Xb1)
Yc1 = max(Ya1,Yb1)
Xc2 = min(Xa2,Xb2)
Yc2 = min(Ya2,Yb2)
这样就求出了矩形的相交区域。
另外,注意到在不假设矩形相交的前提下,定义(Xc1,Yc1),(Xc2,Yc2),且Xc1,Yc1,Xc2,Yc2的值由上面四个式子得出。这样, 可以依据Xc1,Yc1,Xc2,Yc2的值来判断矩形相交。
Xc1,Yc1,Xc2,Yc2只要同时满足下面两个式子,就可以说明两个矩形相交。
3) Xc1 <= Xc2
4) Yc1 <= Yc2
即:
max(Xa1,Xb1) <= min(Xa2,Xb2)
max(Ya1,Yb1) <= min(Ya2,Yb2)
