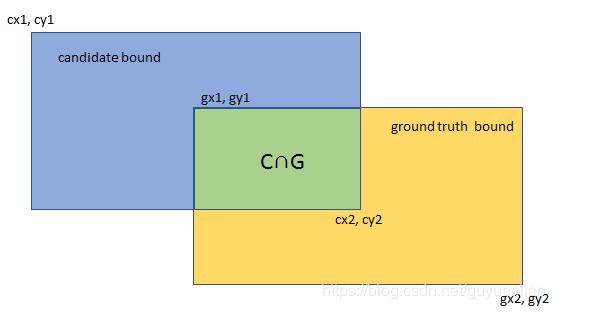
交并比(Intersection-over-Union,IoU),目标检测中使用的一个概念,是产生的候选框(candidate bound)与原标记框(ground truth bound)的交叠率,即它们的交集与并集的比值。最理想情况是完全重叠,即比值为1。
计算公式:
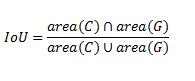
Python实现代码:
def cal_iou(box1, box2): """ :param box1: = [xmin1, ymin1, xmax1, ymax1] :param box2: = [xmin2, ymin2, xmax2, ymax2] :return: """ xmin1, ymin1, xmax1, ymax1 = box1 xmin2, ymin2, xmax2, ymax2 = box2 # 计算每个矩形的面积 s1 = (xmax1 - xmin1) * (ymax1 - ymin1) # C的面积 s2 = (xmax2 - xmin2) * (ymax2 - ymin2) # G的面积 # 计算相交矩形 xmin = max(xmin1, xmin2) ymin = max(ymin1, ymin2) xmax = min(xmax1, xmax2) ymax = min(ymax1, ymax2) w = max(0, xmax - xmin) h = max(0, ymax - ymin) area = w * h # C∩G的面积 iou = area / (s1 + s2 - area) return iou
# -*-coding: utf-8 -*- """ @Project: IOU @File : IOU.py @Author : panjq @E-mail : pan_jinquan@163.com @Date : 2018-10-14 10:44:06 """ def calIOU_V1(rec1, rec2): """ computing IoU :param rec1: (y0, x0, y1, x1), which reflects (top, left, bottom, right) :param rec2: (y0, x0, y1, x1) :return: scala value of IoU """ # 计算每个矩形的面积 S_rec1 = (rec1[2] - rec1[0]) * (rec1[3] - rec1[1]) S_rec2 = (rec2[2] - rec2[0]) * (rec2[3] - rec2[1]) # computing the sum_area sum_area = S_rec1 + S_rec2 # find the each edge of intersect rectangle left_line = max(rec1[1], rec2[1]) right_line = min(rec1[3], rec2[3]) top_line = max(rec1[0], rec2[0]) bottom_line = min(rec1[2], rec2[2]) # judge if there is an intersect if left_line >= right_line or top_line >= bottom_line: return 0 else: intersect = (right_line - left_line) * (bottom_line - top_line) return intersect/(sum_area - intersect) def calIOU_V2(rec1, rec2): """ computing IoU :param rec1: (y0, x0, y1, x1), which reflects (top, left, bottom, right) :param rec2: (y0, x0, y1, x1) :return: scala value of IoU """ # cx1 = rec1[0] # cy1 = rec1[1] # cx2 = rec1[2] # cy2 = rec1[3] # gx1 = rec2[0] # gy1 = rec2[1] # gx2 = rec2[2] # gy2 = rec2[3] cx1,cy1,cx2,cy2=rec1 gx1,gy1,gx2,gy2=rec2 # 计算每个矩形的面积 S_rec1 = (cx2 - cx1) * (cy2 - cy1) # C的面积 S_rec2 = (gx2 - gx1) * (gy2 - gy1) # G的面积 # 计算相交矩形 x1 = max(cx1, gx1) y1 = max(cy1, gy1) x2 = min(cx2, gx2) y2 = min(cy2, gy2) w = max(0, x2 - x1) h = max(0, y2 - y1) area = w * h # C∩G的面积 iou = area / (S_rec1 + S_rec2 - area) return iou if __name__=='__main__': rect1 = (661, 27, 679, 47) # (top, left, bottom, right) rect2 = (662, 27, 682, 47) iou1 = calIOU_V1(rect1, rect2) iou2 = calIOU_V2(rect1, rect2) print(iou1) print(iou2)
参考:https://www.jb51.net/article/184542.htm
补充知识:Python计算多分类的混淆矩阵,Precision、Recall、f1-score、mIOU等指标
直接上代码,一看很清楚
import os
import numpy as np
from glob import glob
from collections import Counter
def cal_confu_matrix(label, predict, class_num):
confu_list = []
for i in range(class_num):
c = Counter(predict[np.where(label == i)])
single_row = []
for j in range(class_num):
single_row.append(c[j])
confu_list.append(single_row)
return np.array(confu_list).astype(np.int32)
def metrics(confu_mat_total, save_path=None):
'''
:param confu_mat: 总的混淆矩阵
backgound:是否干掉背景
:return: txt写出混淆矩阵, precision,recall,IOU,f-score
'''
class_num = confu_mat_total.shape[0]
confu_mat = confu_mat_total.astype(np.float32) + 0.0001
col_sum = np.sum(confu_mat, axis=1) # 按行求和
raw_sum = np.sum(confu_mat, axis=0) # 每一列的数量
'''计算各类面积比,以求OA值'''
oa = 0
for i in range(class_num):
oa = oa + confu_mat[i, i]
oa = oa / confu_mat.sum()
'''Kappa'''
pe_fz = 0
for i in range(class_num):
pe_fz += col_sum[i] * raw_sum[i]
pe = pe_fz / (np.sum(confu_mat) * np.sum(confu_mat))
kappa = (oa - pe) / (1 - pe)
# 将混淆矩阵写入excel中
TP = [] # 识别中每类分类正确的个数
for i in range(class_num):
TP.append(confu_mat[i, i])
# 计算f1-score
TP = np.array(TP)
FN = col_sum - TP
FP = raw_sum - TP
# 计算并写出precision,recall, f1-score,f1-m以及mIOU
f1_m = []
iou_m = []
for i in range(class_num):
# 写出f1-score
f1 = TP[i] * 2 / (TP[i] * 2 + FP[i] + FN[i])
f1_m.append(f1)
iou = TP[i] / (TP[i] + FP[i] + FN[i])
iou_m.append(iou)
f1_m = np.array(f1_m)
iou_m = np.array(iou_m)
if save_path is not None:
with open(save_path + 'accuracy.txt', 'w') as f:
f.write('OA:\t%.4f\n' % (oa*100))
f.write('kappa:\t%.4f\n' % (kappa*100))
f.write('mf1-score:\t%.4f\n' % (np.mean(f1_m)*100))
f.write('mIou:\t%.4f\n' % (np.mean(iou_m)*100))
# 写出precision
f.write('precision:\n')
for i in range(class_num):
f.write('%.4f\t' % (float(TP[i]/raw_sum[i])*100))
f.write('\n')
# 写出recall
f.write('recall:\n')
for i in range(class_num):
f.write('%.4f\t' % (float(TP[i] / col_sum[i])*100))
f.write('\n')
# 写出f1-score
f.write('f1-score:\n')
for i in range(class_num):
f.write('%.4f\t' % (float(f1_m[i])*100))
f.write('\n')
# 写出 IOU
f.write('Iou:\n')
for i in range(class_num):
f.write('%.4f\t' % (float(iou_m[i])*100))
f.write('\n')
以上这篇python实现交并比IOU教程就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持脚本之家。