本文实例为大家分享了unity绘制一条流动弧线的具体代码,供大家参考,具体内容如下
最终效果

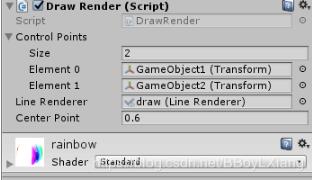
把下面脚本复制,直接拖上脚本,设置两个点(物体)的位置
GameObject1是开始点的位置,GameObject2是结束点的位置
public Transform[] controlPoints;
public LineRenderer lineRenderer;
public float centerPoint =0.1f;
private int layerOrder = 0;
//生成弧线中间的点数
private int _segmentNum = 20;
//偏移
float m_offset;
float m_speed = 0.5f;
void Start()
{
if (!lineRenderer)
{
lineRenderer = GetComponent<LineRenderer>();
}
lineRenderer.sortingLayerID = layerOrder;
//调用画贝斯尔线
GetBeizerList(controlPoints[0].position, (controlPoints[0].position + controlPoints[1].position) * 0.5f + new Vector3(0, centerPoint, 0), controlPoints[1].transform.position, _segmentNum);
}
private void Update()
{
m_offset = m_offset - m_speed * Time.deltaTime;
//控制offset使材质移动
GetComponent<LineRenderer>().material.mainTextureOffset = new Vector2(m_offset, 0);
}
/// <summary>
/// 根据T值,计算贝塞尔曲线上面相对应的点
/// </summary>
/// <param name="t"></param>T值
/// <param name="p0"></param>起始点
/// <param name="p1"></param>控制点
/// <param name="p2"></param>目标点
/// <returns></returns>根据T值计算出来的贝赛尔曲线点
private static Vector3 CalculateCubicBezierPoint(float t, Vector3 p0, Vector3 p1, Vector3 p2)
{
float u = 1 - t;
float tt = t * t;
float uu = u * u;
Vector3 p = uu * p0;
p += 2 * u * t * p1;
p += tt * p2;
return p;
}
/// <summary>
/// 获取存储贝塞尔曲线点的数组
/// </summary>
/// <param name="startPoint"></param>起始点
/// <param name="controlPoint"></param>控制点
/// <param name="endPoint"></param>目标点
/// <param name="segmentNum"></param>采样点的数量
/// <returns></returns>存储贝塞尔曲线点的数组
public Vector3[] GetBeizerList(Vector3 startPoint, Vector3 controlPoint, Vector3 endPoint, int segmentNum)
{
Vector3[] path = new Vector3[segmentNum];
for (int i = 1; i <= segmentNum; i++)
{
float t = i / (float)segmentNum;
Vector3 pixel = CalculateCubicBezierPoint(t, startPoint,
controlPoint, endPoint);
//设置lineRenderer的control Points
lineRenderer.positionCount = i;
lineRenderer.SetPosition(i - 1, pixel);
//存储Point
path[i - 1] = pixel;
Debug.Log(path[i - 1]);
}
return path;
}
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持脚本之家。