二进制和十六进制对于程序员来说应该是很熟悉的东西了,我也不知道为什么我现在还在看这个呢?^_^
什么是二进制?什么是十六进制?
说到进制我们最熟悉的莫过于十进制了,我们从小学的数学都是用的十进制。所谓十进制就是逢十进一,从0开始数 0、1、2、3、.....7、8、9,十个数了再下一个数就要进一位变成10(变成了两位数)。二进制就是逢二进一,0、1再下一个数就要进一位了变成10(变成两位数),十六进制数的道理也是一样的,从0开始数,0、1、2、.....7、8、9发现还没到十六个数还不能进一位,所以不能变成10,那怎么办?数字不够用那就用字母来凑,9后面接着数A、B、C、D、E、F,然后才进一位变成10。
进制间的转换
人类习惯看十进制的数,看到一长串的二进制数就一脸懵逼。计算机就只认二进制的数,看到十进制也是一脸懵逼。至于十六进制我想就是为了取个平衡吧(十六进制和二进制的转换会容易些)。
什么叫进制的转换呢?比如说二进制中0、1后面的数是10(不读作“十”),我们知道在十进制中1后面是2,所以二进制中的10转换为十进制就是2,反过来十进制中的2转换为二进制就是10。当然进制间转换不能靠数。
先从简单的二进制转十六进制说起:比如二进制101010110
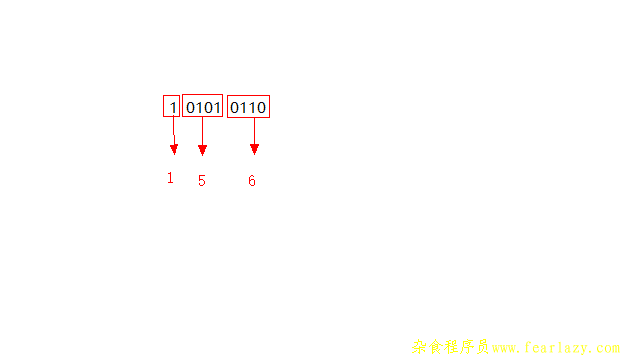
如图所示:将二进制每四位分为一组,不够四位的前面补0(例子中没补)。每一组都可以转换为一个十六进制的数,将这些数连在一起就是结果,也就是说上面的二进制转换位十六进制为156。那么每一个组里的二进制要怎么转为十六进制呢?
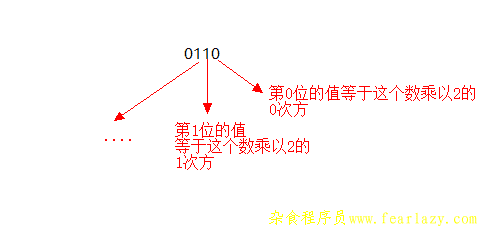
从上图可知0110的值计算为0*8 + 1*4 + 1*2 + 0*1 = 6。如果4位全为1刚好是十六进制的F,这可以解释为什么是4位划分为一组了。
十六进制转二进制刚好是一个相反的过程。将十六进制数的每一位转化为一个4位的二进制,然后连起来。
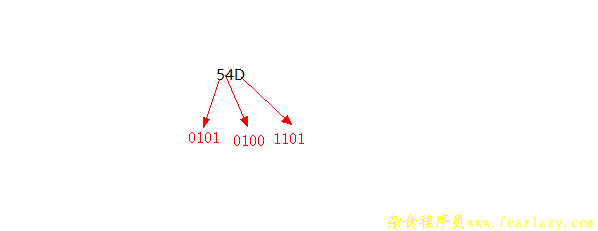
二进制转十进制的思路第二幅图的思路是一样的,只不过不分组就是了。例:
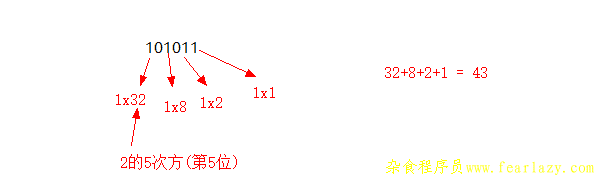
十进制转二进制就比较麻烦了,要将十进制的数不断除2取余数,懒得写了丢个网上的图片:
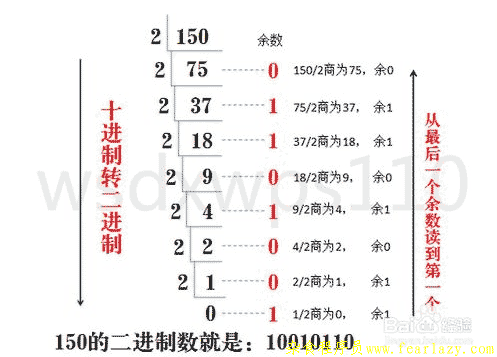
下面是其他网友的补充
1.十进制转R进制1.1 十进制转二进制
十进制整数转二进制
十进制整数转换成二进制采用“除2倒取余”,十进制小数转换成二进制小数采用“乘2取整”。
例题: 135D = ______ B
**解析:**如下图所示,将135除以2,得余数,直到不能整除,然后再将余数从下至上倒取。得到结果:1000 0111B.
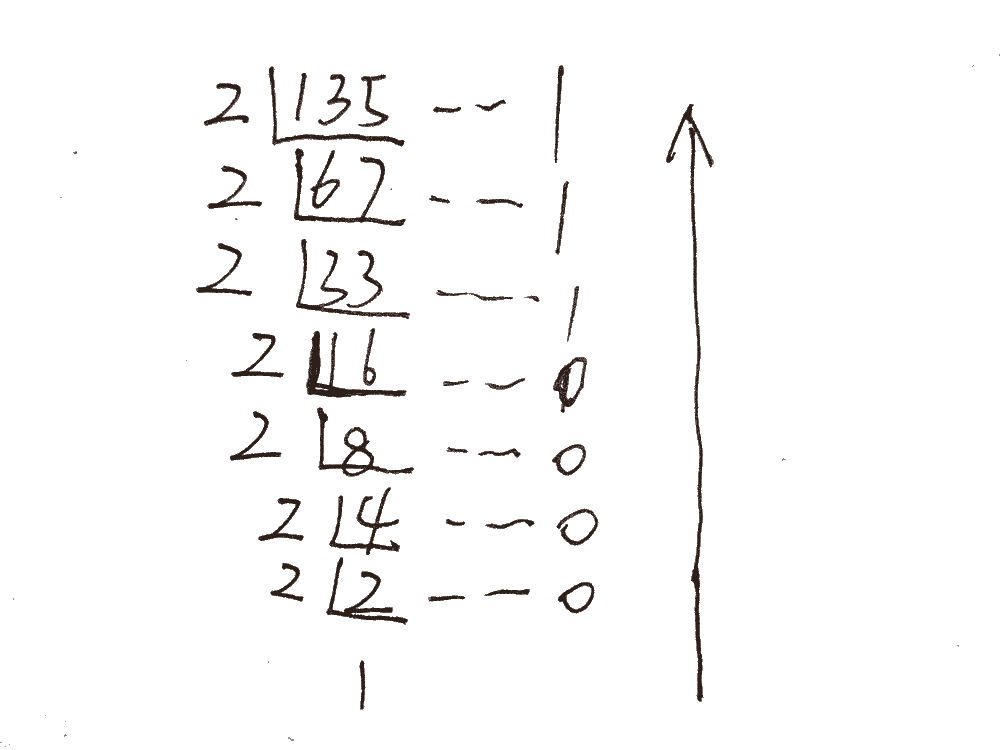
十进制小数转二进制
十进制小数转换成二进制小数采用 “乘2取整,顺序排列” 法。
具体做法是:
用2乘十进制小数,可以得到积,将积的整数部分取出,再用2乘余下的小数 部分,又得到一个积,再将积的整数部分取出,如此进行,直到积中的小数部分为零,或者达到所要求的精度为止。
然后把取出的整数部分按顺序排列起来,先取的整数作为二进制小数的高位有效位,后取的整数作为低位有效位。
例题: 0.68D = ______ B(精确到小数点后5位)
**解析:**如下图所示,0.68乘以2,取整,然后再将小数乘以2,取整,直到达到题目要求精度。得到结果:0.10101B.
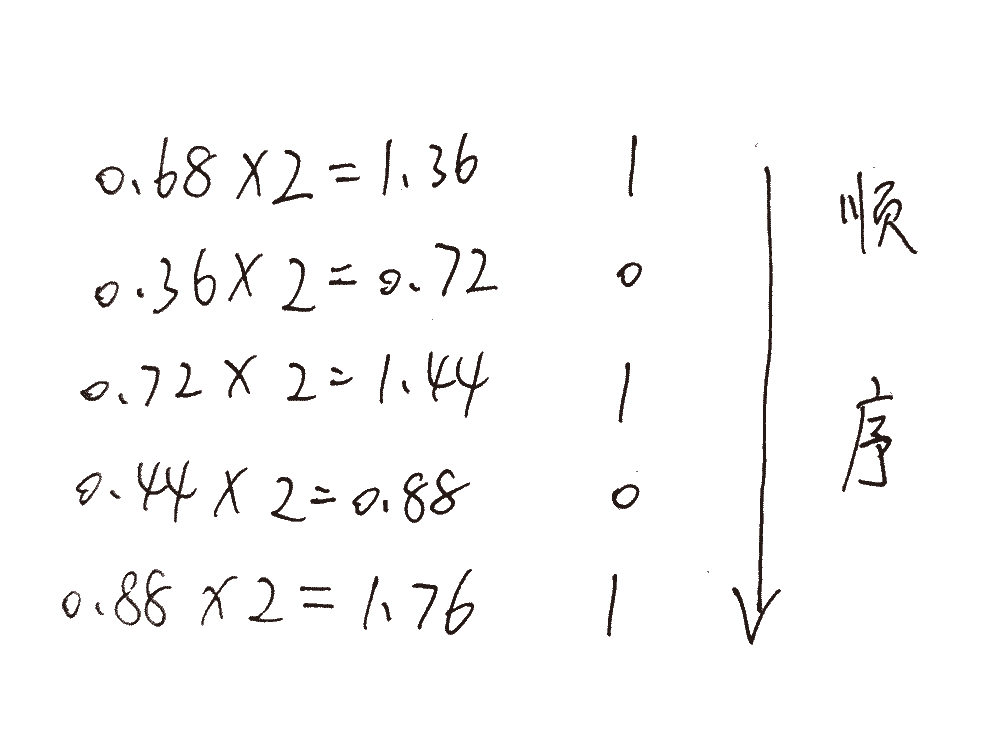
1.2 十进制转八进制
思路和十进制转二进制一样,参考如下例题:
例题: 10.68D = ______ Q(精确到小数点后3位)
**解析:**如下图所示,整数部分除以8取余数,直到无法整除。小数部分0.68乘以8,取整,然后再将小数乘以8,取整,直到达到题目要求精度。得到结果:12.534Q.

1.3 十进制转十六进制
思路和十进制转二进制一样,参考如下例题:
例题: 25.68D = ______ H(精确到小数点后3位)
**解析:**如下图所示,整数部分除以16取余数,直到无法整除。小数部分0.68乘以16,取整,然后再将小数乘以16,取整,直到达到题目要求精度。得到结果:19.ae1H.
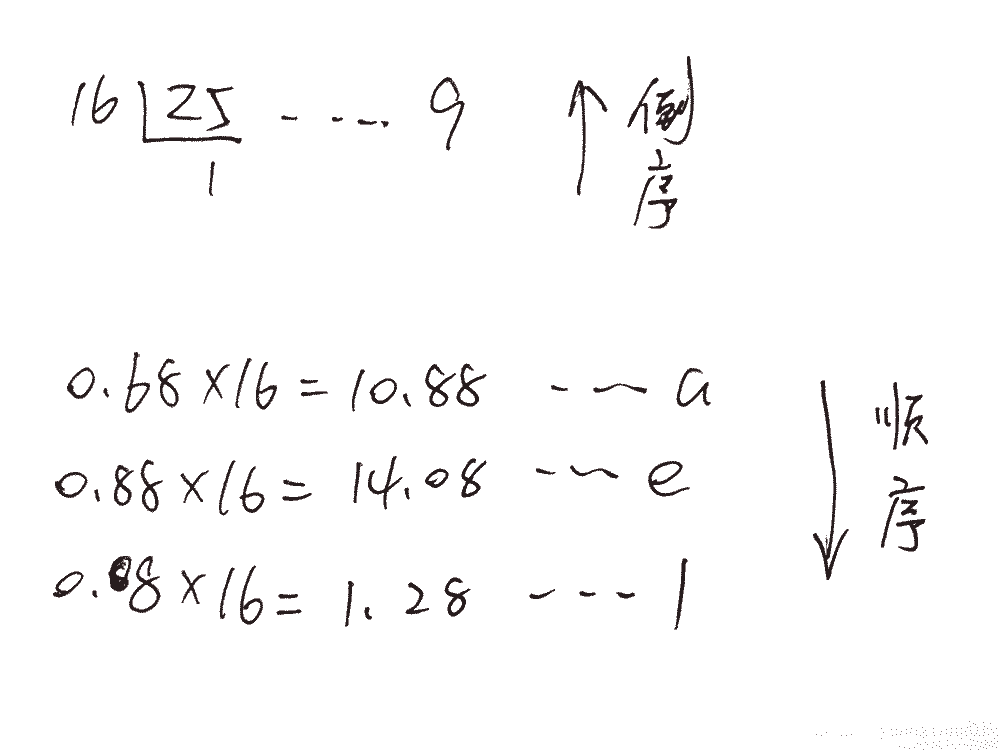
# 2.R进制转十进制## 2.1 二进制转十进制**方法为:**把二进制数按权展开、相加即得十进制数。(具体用法如下图)
例题: 1001 0110B = ______ D
**解析:**如下图所示。得到结果:150D.
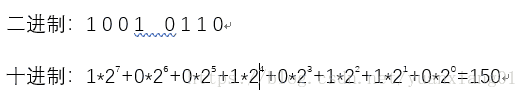
2.2 八进制转十进制
八进制转十进制的方法和二进制转十进制一样。
例题: 26Q = ______ D
**解析:**如下图所示。得到结果:22D.
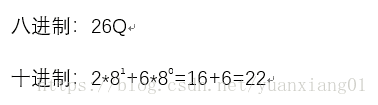
2.3 十六进制转十进制
例题: 23daH = ______ D
**解析:**如下图所示。得到结果:9178D.

3.二进制转八进制
二进制转换成八进制的方法是,取三合一法,即从二进制的小数点为分界点,向左(或向右)每三位取成一位。
例题: 1010 0100B = ____Q
**解析:**计算过程如下图所示。得到结果:244Q.

4.二进制转十六进制
二进制转换成八进制的方法是,取四合一法,即从二进制的小数点为分界点,向左(或向右)每四位取成一位。
例题: 1010 0100B = ____H
**解析:**计算过程如下图所示。得到结果:a4H.

5.工欲善其事,必先利其器
下面的表格是8位二进制所对应的十进制数值,对进制转换以及类似题目的理解非常有用:
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | B |
|---|---|---|---|---|---|---|---|---|
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | D |
注:B:二进制
D:十进制
例题: 135D = ______ B
**解析:**有了上面二进制对应十进制数值的表格,我们就可以将题目给的十进制135拆分为:128+7,再从表格中找到对应的数值,拼凑即可得到答案。
135D = 128D + 7D = 1000 0111B
作者:戴翔
电子邮箱:daixiangcn@outlook.com
简介:中华人民共和国公民,中国共青团员,CSDN博客专家,秦淮区疾控中心托管社会公益组织指南针工作室志愿者,创业公司研发中心负责人,在校大学生。