我就废话不多说了,大家还是直接看代码吧!
import numpy as np
#已知平行四边形三个点,求第四个点
#计算两点之间的距离
def CalcEuclideanDistance(point1,point2):
vec1 = np.array(point1)
vec2 = np.array(point2)
distance = np.linalg.norm(vec1 - vec2)
return distance
#计算第四个点
def CalcFourthPoint(point1,point2,point3): #pint3为A点
D = (point1[0]+point2[0]-point3[0],point1[1]+point2[1]-point3[1])
return D
#三点构成一个三角形,利用两点之间的距离,判断邻边AB和AC,利用向量法以及平行四边形法则,可以求得第四个点D
def JudgeBeveling(point1,point2,point3):
dist1 = CalcEuclideanDistance(point1,point2)
dist2 = CalcEuclideanDistance(point1,point3)
dist3 = CalcEuclideanDistance(point2,point3)
dist = [dist1, dist2, dist3]
max_dist = dist.index(max(dist))
if max_dist == 0:
D = CalcFourthPoint(point1,point2,point3)
elif max_dist == 1:
D = CalcFourthPoint(point1,point3,point2)
else:
D = CalcFourthPoint(point2,point3,point1)
return D
print(JudgeBeveling((0,1),(1,0),(1,1)))
print(JudgeBeveling((5,39),(500,35),(496,17)))
补充知识:计算图像中任意四个点连成的四边形面积与Ground truth的IOU(Python)
1.先求任意四个点连成四边形的面积
这个问题可以用下面的图简单的看一下
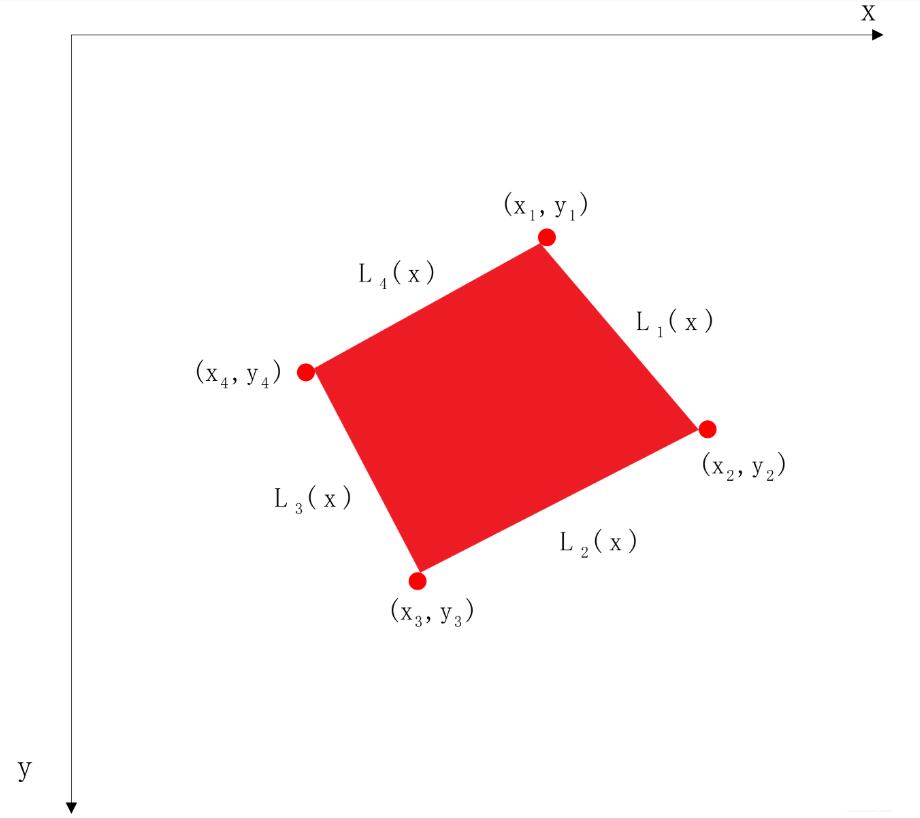
图像的坐标如上图所示,大致的想法就是四个点可以确定四条线,然后进行判断,在红色区域中则为面积中的一个像素,否则不在。先求四条线的斜率
def line_slope(x1,y1,x2,y2,x3,y3,x4,y4):
k1=(y2-y1)/(x2-x1)
k2=(y3-y2)/(x3-x2)
k3=(y4-y3)/(x4-x3)
k4=(y1-y4)/(x1-x4)
return k1,k2,k3,k4
然后计算每个位置上的各个函数值
l1=int(tk1*(i-tx1)+ty1)
l2=int(tk2*(i-tx2)+ty2)
l3=int(tk3*(i-tx3)+ty3)
l4=int(tk4*(i-tx4)+ty4)
判断条件很重要,因为左边是那样排列的,所以判断条件就是
(l1<=j)&(l2>=j)&(l3>=j)&(l4<=j)
也就是在红色区域中任取一点都满足这个条件。定义一个全局变量,满足条件就+1。面积就求出来了。
其实求面积并不是我的目的
2.求相交的面积
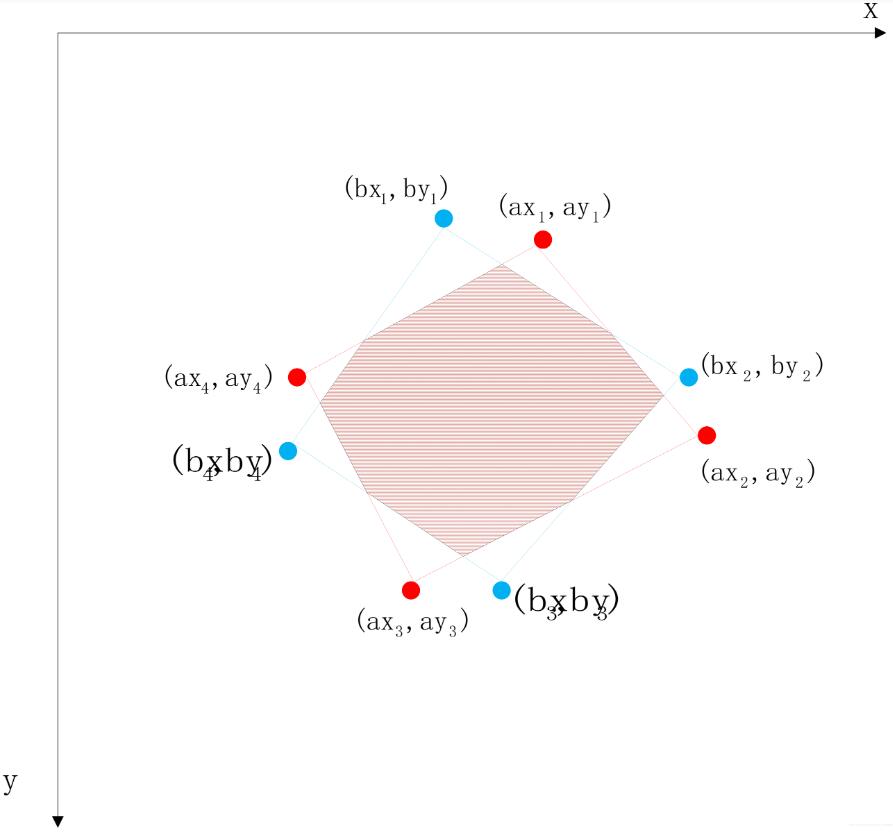
两个面积分别求出来以后,两个面积的交集面积最简单的可以通过对照两个区域的坐标进行求解。
也就是在分别计算两个面积的时候记下符合条件的坐标(x,y)存放到数组中,最后比较两个数组中相等的元素的个数即可求解。
3.并面积
交的面积计算完后,可以用下面的公式(S1:四边形1的面积、S2:四边形2的面积、iu:交面积)
并面积=S1-iu+S2
4.IOU
交面积/并面积
5.测试
(1)

(2)

(3)

可以看到最后一种情况红框已经把ground truth包含了,所以可以直接用S2/S1来检验算法的准确性
而13882/19307=0.719013829181126,可以证明算法的准确性。
测试代码:链接
和别的算法进行比较
还是有区别的。。。
v2是向量方法计算
v3是shapely包计算
以上这篇python 已知平行四边形三个点,求第四个点的案例就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持脚本之家。