1、流程
大体流程如下,无论图像、声音、ADC数据都是如下流程:
(1)将原信号进行FFT;
(2)将进行FFT得到的数据去掉需要滤波的频率;
(3)进行FFT逆变换得到信号数据;
2、算法仿真
2.1 生成数据:
#采样点选择1400个,因为设置的信号频率分量最高为600Hz,根据采样定理知采样频率要大于信号频率2倍,所以这里设置采样频率为1400Hz(即一秒内有1400个采样点) x=np.linspace(0,1,1400) #设置需要采样的信号,频率分量有180,390和600 y=2*np.sin(2*np.pi*180*x) + 3*np.sin(2*np.pi*390*x)+4*np.sin(2*np.pi*600*x)
2.2 对生成的数据进行FFT变换
yy=fft(y) #快速傅里叶变换 yf=abs(fft(y)) # 取模 yf1=abs(fft(y))/((len(x)/2)) #归一化处理 yf2 = yf1[range(int(len(x)/2))] #由于对称性,只取一半区间
2.3显示转换结果:
显示原始FFT模值:
#混合波的FFT(双边频率范围)
plt.figure(2)
plt.plot(xf,yf,'r') #显示原始信号的FFT模值
plt.title('FFT of Mixed wave(two sides frequency range)',fontsize=7,color='#7A378B') #注意这里的颜色可以查询颜色代码表
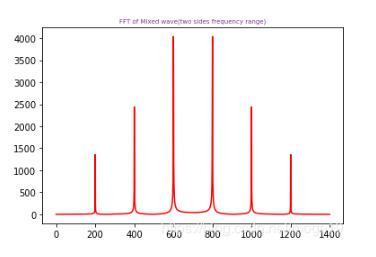
显示原始FFT归一化后的模值:
#混合波的FFT(归一化)
plt.figure(3)
plt.plot(xf1,yf1,'g')
plt.title('FFT of Mixed wave(normalization)',fontsize=9,color='r')
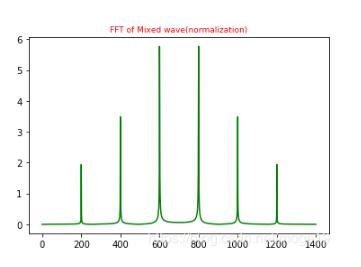
由于对称,只取一半区间进行显示
plt.figure(4)
plt.plot(xf2,yf2,'b')
plt.title('FFT of Mixed wave)',fontsize=10,color='#F08080')
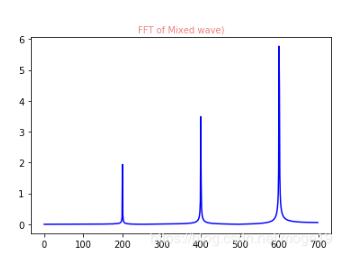
3、利用FFT进行滤波
例如将频率为600HZ的噪声滤掉,这里直接将该频段的数据置零:
yy=fft(y) #快速傅里叶变换
yreal = yy.real # 获取实数部分
yimag = yy.imag # 获取虚数部分
test_y =yy
for i in range(len(yy)):
if i <=900 and i>=500:
test_y[i]=0
对置零后的数据进行逆变换:
test = np.fft.ifft(test_y) #对变换后的结果应用ifft函数,应该可以近似地还原初始信号。
对还原的数据进行FFT变换的结果:
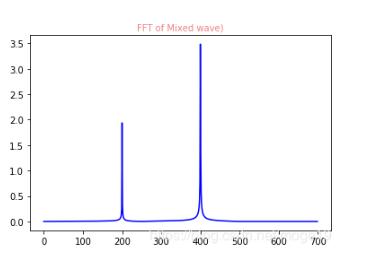
滤波后的数据和原数据相对比:
蓝色的为原数据,橙色的为滤波后的数据

假设将400Hz和600Hz的信号都滤掉得到的信号图像如下:
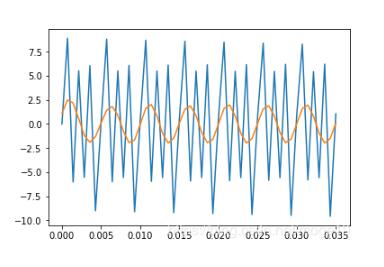
4、对随机噪声进行滤波
源码:
noise_size = 1400
noise_array = np.random.normal(0, 2, noise_size)
adc_value=[]
for i in range(noise_size):
adc_value.append(0)
y= np.array(adc_value) + noise_array
yy=fft(y) #快速傅里叶变换
yf=abs(fft(y)) # 取模
yf1=abs(fft(y))/((len(y)/2)) #归一化处理
yf2 = yf1[range(int(len(y)/2))] #由于对称性,只取一半区间
#混合波的FFT(双边频率范围)
xf = np.arange(len(y))
plt.figure(1)
plt.plot(xf,yf,'r') #显示原始信号的FFT模值
plt.title('FFT of Mixed wave(two sides frequency range)',fontsize=7,color='#7A378B') #注意这里的颜色可以查询颜色代码表
yy=fft(y) #快速傅里叶变换
yreal = yy.real # 获取实数部分
yimag = yy.imag # 获取虚数部分
test_y =yy
for i in range(len(yy)):
if i <=1200 and i>=200:
test_y[i]=0
test = np.fft.ifft(test_y) #对变换后的结果应用ifft函数,应该可以近似地还原初始信号。
y=test
yy=fft(y) #快速傅里叶变换
yf=abs(fft(y)) # 取模
yf1=abs(fft(y))/((len(y)/2)) #归一化处理
yf2 = yf1[range(int(len(y)/2))] #由于对称性,只取一半区间
#混合波的FFT(双边频率范围)
xf = np.arange(len(y))
plt.figure(2)
plt.plot(xf,yf,'r') #显示原始信号的FFT模值
plt.title('FFT of Mixed wave(two sides frequency range)',fontsize=7,color='#7A378B') #注意这里的颜色可以查询颜色代码表
运行结果:
原数据频谱图:

滤波后的频谱图:

滤波后(蓝色线)与原数据(红色线)对比:

以上这篇Python利用FFT进行简单滤波的实现就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持脚本之家。